线段树是我最喜欢的数据结构之一了,几乎每一场比赛都能遇到相关的题目,它的强大是有目共睹的。
这篇博客主要是讲讲它的原理及一些应用,顺便提一下线段树的一些应用。
本片博文虽为新手向,但需要你有一定前缀知识,如:
C++语法基础
位运算基础
函数的递归和回溯思想
分治思想(如二分)
基础数据结构(主要为二叉树)
后续还可能会放上讲解可持久化线段树(主席树)的文章(大概
对于经常遇见的这样一类问题:
给你n n n m m m
求某区间的和/最大值/最小值/乘积……
修改某个数字/某个区间段里的数字
……
其中,n n n m m m 10 5 {10}^5 1 0 5
刨去修改,如果只有求区间和/乘积,那么使用前缀和计算将是你最好的选择。
如果是求最大值/最小值,也可以使用DP、RMQ、分块等方式解决。
但是一旦加上修改,上述解决方案都不是很适用,而传统暴力做法的时间复杂度将会高达O ( n ⋅ m ) O(n \cdot m) O ( n ⋅ m )
那么是不是有一种办法可以很好地处理上述问题呢?—— 点我看答案
答案当然是线段树啦!
接下来介绍一下什么是线段树:
线段树是一种二叉搜索树,借助分治算法思想,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个节点。
——改编自百度百科
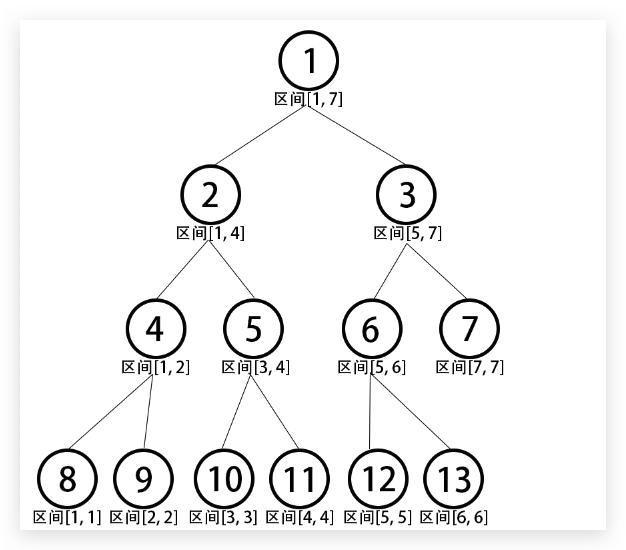
它的结构大概长成这样(图来源百度百科):
树中的每一个节点代表一个区间(或者说一条线段)的信息,以二分区间为左右儿子节点,直到不可再分。
不难发现,线段树上的每一个节点,要么没有儿子节点(此区间不可再分),要么必然有两个儿子节点(类似完全二叉树),这为我们建树操作提供了便利。
点我查看线段树结构问题
在早期时笔者一直听有些人说线段树是棵完全二叉树,但实际上并不一定,完全二叉树的特点是:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部 。例如上面百度百科中提到的线段树结构图片就已经可以看出了,这并不是一棵完全二叉树,区间[ 6 , 6 ] [6, 6] [ 6 , 6 ] [ 7 , 7 ] [7, 7] [ 7 , 7 ]
但线段树可以视为一棵平衡二叉树(树中任意节点的左右子树高度差最大为1 1 1 n n n p p p k k k 至多 在⌊ log 2 n ⌋ + 1 \left\lfloor\log_2{n}\right\rfloor + 1 ⌊ log 2 n ⌋ + 1 至少 在⌊ log 2 n ⌋ \left\lfloor\log_2{n}\right\rfloor ⌊ log 2 n ⌋ 1 1 1
若是利用一个一维数组来模拟这棵线段树,将线段树的节点以层序编号,可以发现编号为p p p 2 ⋅ p 2 \cdot p 2 ⋅ p 2 ⋅ p + 1 2 \cdot p + 1 2 ⋅ p + 1
再利用递归思想,我们可以先将线段树的叶子节点信息(此时区间必然不可分,只需要存单点的值)保存,解决完某个节点信息时便回溯,此时会回到某个父节点,若其两个儿子节点均已回溯,该父节点的信息便为两个儿子节点信息的合并 。
以线段树存储区间和 信息为例,这里贴出建树代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 int a[MAX_N]; int tree[MAX_N << 2 ]; void build (int l, int r, int p) if (l == r) { tree[p] = a[l]; return ; } int mid = (l + r) >> 1 ; build(l, mid, p << 1 ), build(mid + 1 , r, p << 1 | 1 ); tree[p] = tree[p << 1 ] + tree[p << 1 | 1 ]; }
注:这里没有直接使用乘/除法,而是利用了位运算,属于个人习惯,现代编译器会自动讲乘/除2 n 2^n 2 n
这是一个比较粗浅(暴力)的建树方式,也可以以插入节点的方式建树(下文将提及),实际时间复杂度均为O ( n ⋅ log 2 n ) O(n \cdot \log_2n) O ( n ⋅ log 2 n )
需要注意 的两个点:
线段树结构的节点数应以大于等于数据量的满二叉树计算(想想为什么?),所以实际申请的空间大致为最大区间长度的4 4 4
若是合并儿子节点信息的操作比较复杂,可以独立成一个函数方便修改,这里只需要相加,所以直接写在建树里。
点我查看建树时间复杂度及空间复杂度分析
关于建树的时间复杂度分析*:
对于数据量恰好可以构成一棵满二叉树,假设叶子节点数(即数据量)为n n n ( log 2 n ) + 1 (\log_2 n) + 1 ( log 2 n ) + 1 O ( log 2 n ) O(\log_2 n) O ( log 2 n ) n n n 2 x 2^x 2 x ⌈ log 2 n ⌉ \left\lceil\log_2{n}\right\rceil ⌈ log 2 n ⌉ ⌊ log 2 n ⌋ + 1 \left\lfloor\log_2{n}\right\rfloor + 1 ⌊ log 2 n ⌋ + 1 O ( log 2 n ) O(\log_2{n}) O ( log 2 n ) O ( n ⋅ log 2 n ) O(n \cdot \log_2 n) O ( n ⋅ log 2 n )
关于线段树的空间复杂度分析*:
由上述容易分析线段树叶子节点数为2 ⌈ log 2 n ⌉ 2^{\left\lceil\log_2{n}\right\rceil} 2 ⌈ log 2 n ⌉ 2 ⌈ log 2 n ⌉ + 1 − 1 2^{\left\lceil\log_2{n}\right\rceil + 1} - 1 2 ⌈ log 2 n ⌉ + 1 − 1 2 ⌈ log 2 n ⌉ + 1 − 1 2^{\left\lceil\log_2{n}\right\rceil + 1} - 1 2 ⌈ log 2 n ⌉ + 1 − 1 n n n n n n 2 x + 1 2^{x} + 1 2 x + 1 2 ⌈ log 2 n ⌉ + 1 − 1 = 2 x + 2 − 1 = 4 ⋅ n − 5 2^{\left\lceil\log_2{n}\right\rceil + 1} - 1 = 2^{x + 2} - 1 = 4 \cdot n - 5 2 ⌈ log 2 n ⌉ + 1 − 1 = 2 x + 2 − 1 = 4 ⋅ n − 5 4 4 4 O ( n ) O(n) O ( n )
接下来谈谈单点修改,这是线段树中比较简单但很常用的内容。
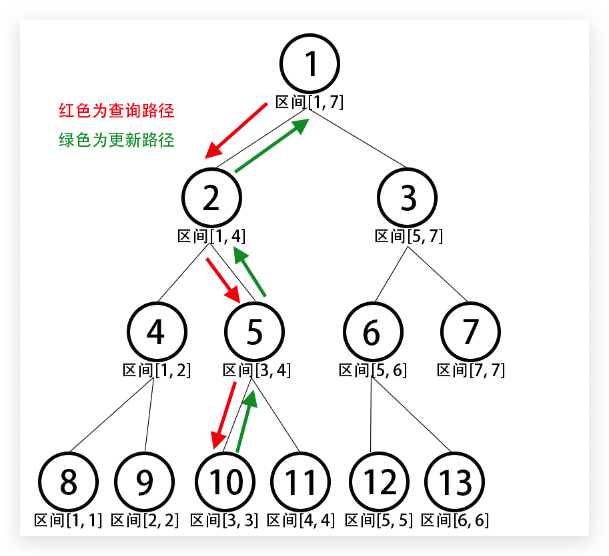
我们假设现在有7 7 7
*圆圈内数字为线段树节点的下标
如果我们要修改第3 3 3 10 10 1 0 不断向上更新,直到根节点 。
那么如何找到这个节点?其实很简单,只需要从根节点开始,判断需要查找的位置k k k [ l , r ] [l, r] [ l , r ] m i d mid m i d
推广到一般情况:建树后,无论我们是要修改哪个位置的值,都只需要向下寻找到需要修改的点,然后回溯更新即可。
下面贴上代码(仍以区间和为例):
1 2 3 4 5 6 7 8 9 10 11 12 void updatePoint (int l, int r, int p, int k, int s) if (l == r && r == k) { tree[p] = s; return ; } int mid = (l + r) >> 1 ; if (mid >= k) updatePoint(l, mid, p << 1 , k, s); else if (mid < k) updatePoint(mid + 1 , r, p << 1 | 1 , k, s); tree[p] = tree[p << 1 ] + tree[p << 1 | 1 ]; return ; }
单点查询与单点修改思想是相同的,即在到达叶子节点时返回这个节点的值,下面贴上代码:
1 2 3 4 5 6 7 8 9 int queryPoint (int l, int r, int p, int k) if (l == r && r == k) { return tree[p]; } int mid = (l + r) >> 1 , ret = -1 ; if (mid >= k) ret = queryPoint(l, mid, p << 1 , k); else if (mid < k) ret = queryPoint(mid + 1 , r, p << 1 | 1 , k); return ret; }
每次单点修改/查询的时间复杂度均为O ( log 2 n ) O(\log_2 n) O ( log 2 n )
点我查看单点/修改查询时间复杂度分析
关于单点修改/单点查询的时间复杂度分析*:
该操作仅会完整地走完树上的一条链,由于线段树是一棵完全二叉树,故其最长链长度与层数相同,为⌊ log 2 n ⌋ + 1 \left\lfloor\log_2{n}\right\rfloor + 1 ⌊ log 2 n ⌋ + 1 n n n O ( log 2 n ) O(\log_2 n) O ( log 2 n )
上文建树部分有提到,我们还可以利用单点修改来建立线段树结构,其实就是对于每个数,将其修改(赋值)到对应位置,即对于数组a a a i i i update(1, n, 1, i, a[i]),那么对于n n n O ( n ⋅ log 2 n ) O(n \cdot \log_2 n) O ( n ⋅ log 2 n )
接下来将涉及线段树结构最核心的思想部分。
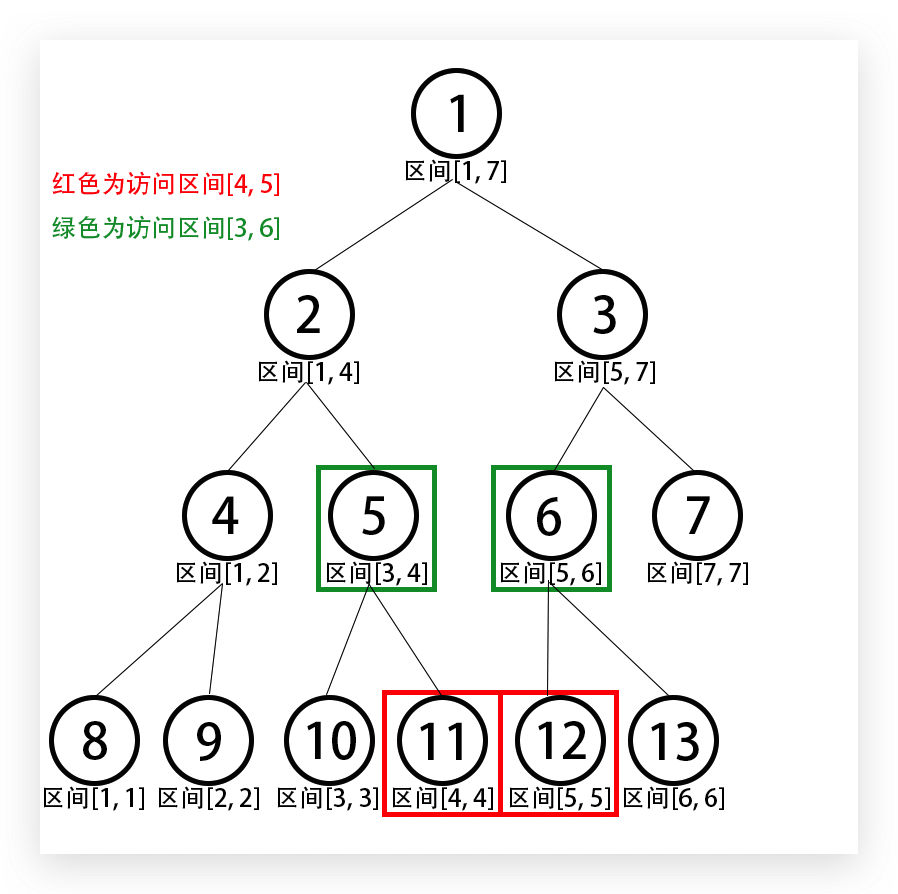
对于查询某个区间的信息,通过观察可以发现我们只需要访问树上某些节点的信息并合并,而不一定走到叶子节点一个一个地访问(反而有些本末倒置),例如在数据量为7 7 7 [ 4 , 5 ] [4,5] [ 4 , 5 ] 11 11 1 1 12 12 1 2 [ 3 , 6 ] [3, 6] [ 3 , 6 ] 5 5 5 6 6 6
那么,怎么才能知道需要的是哪些节点的信息呢?
对于要询问一个区间[ L , R ] [L, R] [ L , R ] p p p [ l , r ] [l, r] [ l , r ] [ L , R ] [L, R] [ L , R ] L ≤ l ≤ r ≤ R L \leq l \leq r \leq R L ≤ l ≤ r ≤ R p p p p p p [ L , R ] [L, R] [ L , R ] [ l , r ] [l, r] [ l , r ] m i d mid m i d [ L , R ] [L, R] [ L , R ] L ≤ m i d L \leq mid L ≤ m i d p p p m i d < R mid < R m i d < R
如模拟在数据量为7 7 7 [ 3 , 6 ] [3, 6] [ 3 , 6 ] 1 1 1 [ 1 , 7 ] [1, 7] [ 1 , 7 ] m i d 1 = ( 1 + 7 ) / 2 = 4 mid_1 = (1 + 7) / 2 = 4 m i d 1 = ( 1 + 7 ) / 2 = 4 3 ≤ m i d 1 = 4 3 \leq mid_1 = 4 3 ≤ m i d 1 = 4 1 1 1 [ 1 , 4 ] [1, 4] [ 1 , 4 ] 1 1 1 2 2 2
此时来到节点2 2 2 [ 1 , 4 ] [1, 4] [ 1 , 4 ] m i d 2 = ⌊ ( 1 + 4 ) / 2 ⌋ = 2 mid_2 = \left\lfloor(1 + 4) / 2 \right\rfloor = 2 m i d 2 = ⌊ ( 1 + 4 ) / 2 ⌋ = 2 3 > m i d 2 = 2 3 > mid_2 = 2 3 > m i d 2 = 2 2 2 2 [ 1 , 2 ] [1, 2] [ 1 , 2 ] m i d 2 = 2 < 6 mid_2 = 2 < 6 m i d 2 = 2 < 6 2 2 2
然后来到了节点5 5 5 [ 3 , 4 ] [3, 4] [ 3 , 4 ] [ 3 , 6 ] [3, 6] [ 3 , 6 ] r e t 1 ret_1 r e t 1 1 1 1 1 1 1 r e t 2 ret_2 r e t 2 r e t 1 ret_1 r e t 1 r e t 2 ret_2 r e t 2 r e t 1 + r e t 2 ret_1 + ret_2 r e t 1 + r e t 2
将上述过程编写为代码如下(以区间求和为例):
1 2 3 4 5 6 7 8 9 10 11 12 void querySeg (int l, int r, int p, int L, int R) if (L <= l && r <= R) { return tree[p]; } int mid = (l + r) >> 1 , ret = 0 ; if (L <= mid) ret += querySeg(l, mid, p << 1 , L, R); if (mid < R) ret += querySeg(mid + 1 , r, p << 1 | 1 , L, R); return ret; }
看到这是不是觉得非常简单?读者可以尝试一下证明区间查询的时间复杂度是不是O ( log 2 n ) O(\log_2{n}) O ( log 2 n )
注:建议先完全掌握区间查询的过程后再学习区间修改。
点我查看区间查询时间复杂度分析
关于区间查询的时间复杂度分析*:
在利用上述过程查找区间[ L , R ] [L, R] [ L , R ] p p p [ l , r ] [l, r] [ l , r ] m i d mid m i d [ L , R ] [L, R] [ L , R ] p p p [ L , m i d ] [L, mid] [ L , m i d ] m i d mid m i d L L L ⌊ log 2 n ⌋ + 1 \left\lfloor\log_2{n}\right\rfloor + 1 ⌊ log 2 n ⌋ + 1
同理,往右子树查询时,就是在查询[ m i d + 1 , R ] [mid + 1, R] [ m i d + 1 , R ] m i d mid m i d R R R ⌊ log 2 n ⌋ \left\lfloor\log_2{n}\right\rfloor ⌊ log 2 n ⌋ 2 ⋅ ⌊ log 2 n ⌋ + 1 2 \cdot \left\lfloor\log_2{n}\right\rfloor + 1 2 ⋅ ⌊ log 2 n ⌋ + 1 O ( log 2 n ) O(\log_2{n}) O ( log 2 n )
当然,在查询的区间长度为1 1 1 O ( log 2 n ) O(\log_2{n}) O ( log 2 n )
注:上述分析过程是笔者较为粗略分析的过程,实际运用中会产生各种常数,可以参考网上关于线段树结构的论文,里面有更详细的时间复杂度证明。
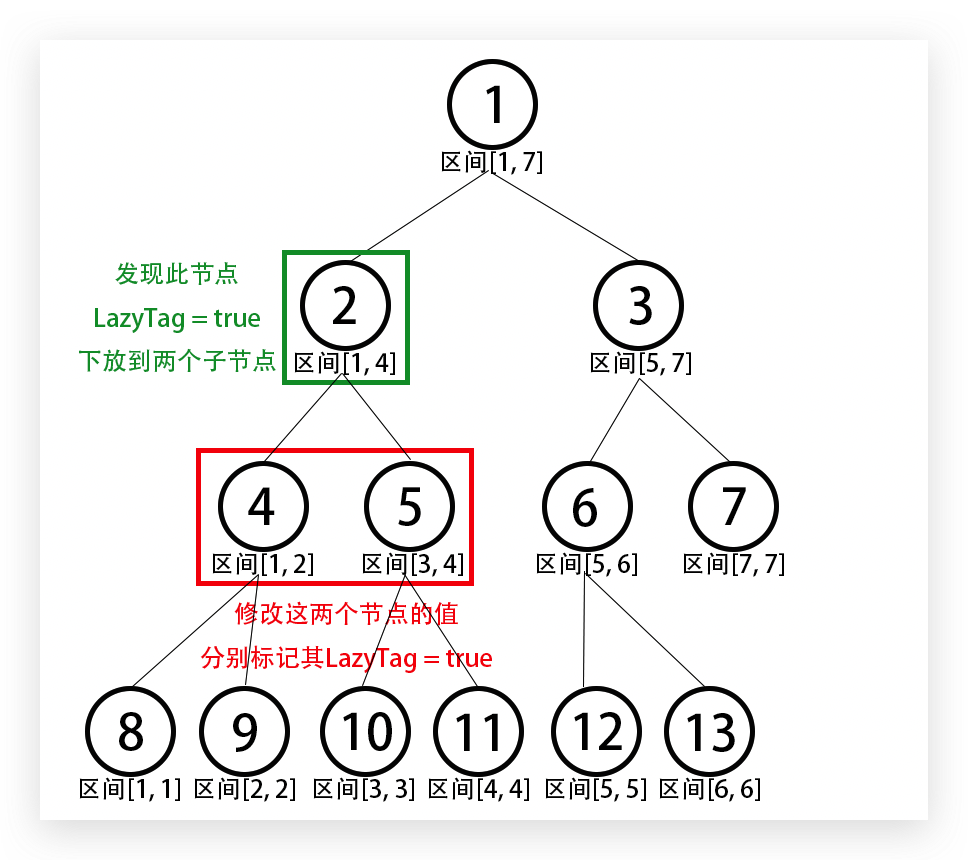
而对于区间修改,则需要引入一个新的概念——懒惰标记(Lazy Tag)。
何谓懒惰标记?其实很简单——就是在要完整修改的区间打上一个标记,说明它被修改过,而此次仅修改该节点的值而不改变其子树的值 ,即此次修改懒惰不修改,下次经过 (有需要修改或查询其子区间时)该点时再将懒惰标记下放到子节点 中(同样是修改子节点的值并打上懒惰标记),这样就可以利用到区间查询的思想去找到需要修改的节点。
举个例子:
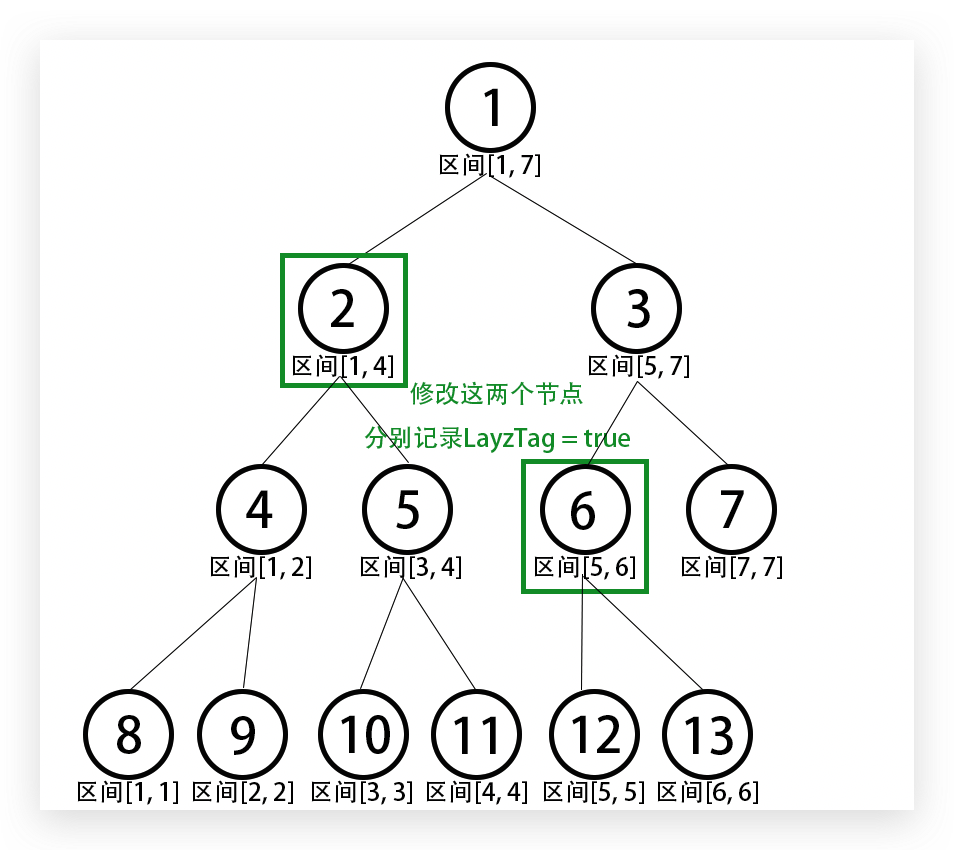
比如在数据量为7 7 7 [ 1 , 6 ] [1, 6] [ 1 , 6 ] 2 2 2 [ 1 , 4 ] [1, 4] [ 1 , 4 ] 6 6 6 [ 5 , 6 ] [5, 6] [ 5 , 6 ]
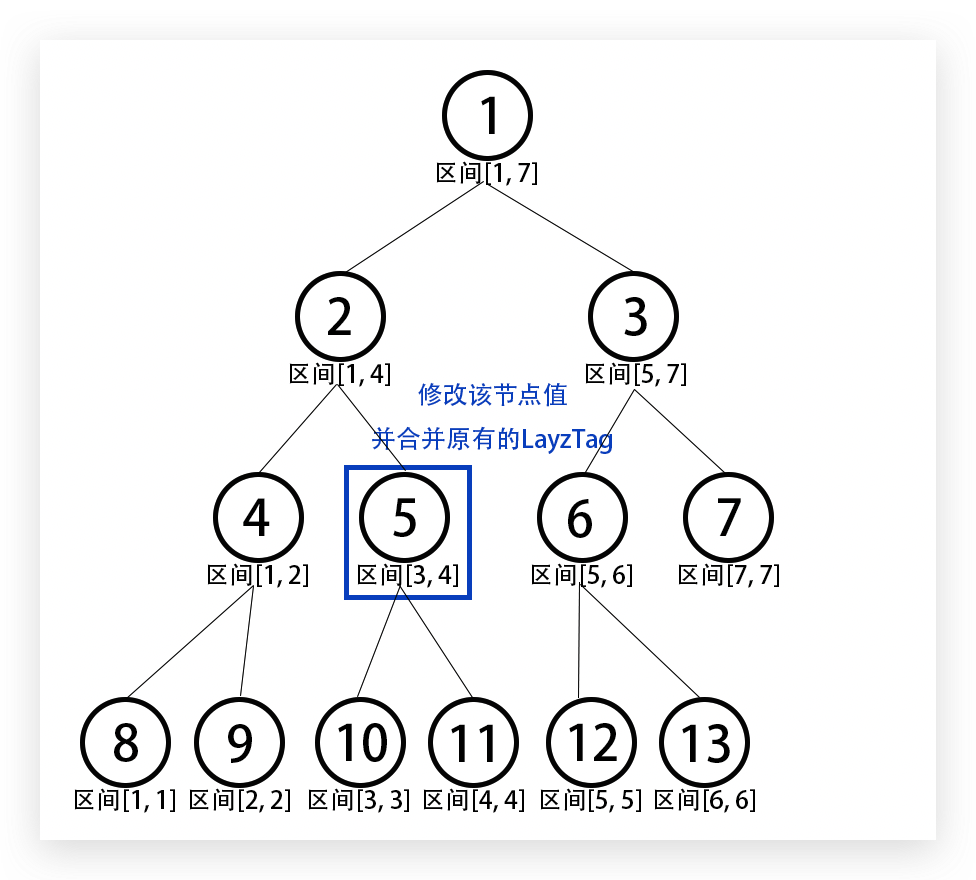
接下来假设要修改区间[ 3 , 4 ] [3, 4] [ 3 , 4 ] 2 2 2 4 4 4 5 5 5 清空 节点2 2 2
这时候继续向下,发现节点5 5 5 [ 3 , 4 ] [3, 4] [ 3 , 4 ]
最后一路往上合并节点值。
将上述过程编写成代码大致如下(以区间求和、修改操作是对区间所有数加上某个值为例):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 int tree[MAX_N], lazy[MAX_N]; void pushDown (int l, int r, int p) if (lazy[p] != 0 ) { int mid = (l + r) >> 1 ; tree[p << 1 ] += (mid - l + 1 ) * lazy[p]; tree[p << 1 | 1 ] += (r - mid) * lazy[p]; lazy[p << 1 ] += lazy[p]; lazy[p << 1 | 1 ] += layz[p]; layz[p] = 0 ; } } void updateSeg (int l, int r, int p, int L, int R, int s) if (L <= l && r <= R) { tree[p] += (r - l + 1 ) * s; lazy[p] += s; return ; } pushDown(l, r, p); int mid = (l + r) >> 1 ; if (L <= mid) updateSeg(l, mid, p << 1 , L, R, s); if (mid < R) updateSeg(mid + 1 , r, p << 1 | 1 , L, R, s); tree[p] = tree[p << 1 ] + tree[p << 1 | 1 ]; }
注:有带懒惰标记的区间修改中,对于单点修改/查询、区间查询操作也需要先下放懒惰标记再往下查询,此处略去代码。
如果你完全掌握了上面讲到的内容,那么可以说明你已经学会线段树的构造和基本使用方法,这边列举几个简单题:
下面再提一道简单的、但看起来不那么像线段树的题目。
传送门 Vjudge
给你一个初始的数字x = 1 x = 1 x = 1 [ 1 , 10 9 ] [1, {10}^{9}] [ 1 , 1 0 9 ] M M M 0 ≤ Q ≤ 10 5 0 \leq Q \leq {10}^{5} 0 ≤ Q ≤ 1 0 5 i i i
M y i y_i y i x x x y i y_i y i 1 ≤ y i ≤ 10 9 1 \leq y_i \leq {10}^{9} 1 ≤ y i ≤ 1 0 9
D d i d_i d i x x x y d i y_{d_i} y d i
爆炸每次D操作的y d i y_{d_i} y d i x % M x \% M x % M
本题来源为第九届福建省大学生程序设计竞赛,也是笔者参加的第一场ICPC形式的比赛,印象深刻。
初看本题,如果读者学过数论,那么很容易往求逆元的方向思考,但题目给的模数M M M x x x M M M
接下来可以发现利用线段树可以算区间乘法的思路来解决这个问题:初始化一棵数据量为Q Q Q 1 1 1 1 1 1 x x x i i i [ i , i ] [i, i] [ i , i ] y i y_i y i [ i , i ] [i, i] [ i , i ] 1 1 1
每次操作的答案都是线段树的根节点,代码这里就不写了,希望读者可以自己实现。
如果将笔者列举出的线段树例题均独立完成后,相信读者已经对线段树模板有了一定自己的理解,但线段树其实只是个模型(实际上任何算法、数据结构都是),更多的还是需要读者自己思考如何利用线段树解决问题。
关于线段树学习的重点主要就是以下两点:
笔者认为对于某些能用线段树解决的题目,这个题目必然满足:支持将数据进行区间二分,并且可以根据二分得到的两个子区间合并得到当前区间的信息(并不一定要支持修改)。
线段树对于解决实际问题并没有太大帮助,在生活中更多地还是利用红黑树或者其他平衡树,但笔者认为学习好线段树是学其他平衡树需要的前缀知识,它相较于其他的平衡树更好实现,在学习的过程中也会把二叉树结构理解得更透彻,并且在算法竞赛中也经常使用。
接下来提一个线段树较为另类的应用。
线段树的变化方式多种多样,这是相对特殊的一种,也可以算是学习可持久化线段树(或者说任何可持久化数据结构)的前缀知识。顾名思义,这棵线段树的节点存的是某种权值,比较常用的是存储区间内各个数字出现的个数(类似桶排序)。
注意:这里提到的区间指的是数值大小而非数据量的区间。
那么有什么用呢?这里举个例题,假设有一个由n ( 1 ≤ n ≤ 10 5 ) n(1 \leq n \leq {10}^{5}) n ( 1 ≤ n ≤ 1 0 5 ) a ( a i ≤ 10 5 ) a (a_i \leq {10}^5) a ( a i ≤ 1 0 5 )
这里可以利用单点修改的思想,初始化一颗数据量为max ( a ) \max(a) max ( a ) 0 0 0 i ∈ 1 → n i \in 1 \to n i ∈ 1 → n [ a i + 1 , max ( a ) ] [a_i + 1, \max(a)] [ a i + 1 , max ( a ) ] [ 1 , i ] [1, i] [ 1 , i ] a i a_i a i i i i s u m i sum_i s u m i a i a_i a i a n s = ∑ i = 1 n s u m i ans = \sum_{i=1}^{n} {sum_i} a n s = ∑ i = 1 n s u m i
当然,如果a i ≤ 10 9 a_i \leq {10}^{9} a i ≤ 1 0 9 max ( a ) \max(a) max ( a ) map)来缩小数据范围,便可以实现此算法,这里就不展开讲如何离散化了。
这个应用相信读者并不难理解,关键点在于可以利用元素加入线段树的顺序来求得一个[ 1 , i ] [1,i] [ 1 , i ]
这里留一个思考题给笔者:给定由n ( 1 ≤ n ≤ 10 5 ) n(1 \leq n \leq {10}^{5}) n ( 1 ≤ n ≤ 1 0 5 ) a ( a i ≤ 10 5 ) a (a_i \leq {10}^5) a ( a i ≤ 1 0 5 ) 1 ≤ i < j < k ≤ n 1 \leq i < j < k \leq n 1 ≤ i < j < k ≤ n a i < a j < a k a_i < a_j < a_k a i < a j < a k a a a
那么到这里,笔者对于线段树的理解就已经基本讲完了,下一篇将谈谈一些特殊的线段树(如zkw)及树状数组。





![[算法] 浅讲线段树和树状数组(一)](https://pic.rmb.bdstatic.com/bjh/cfde8718407f5f3bc0e2a652e50705ff.png)


![[题解] 头脑风暴专题](https://ae01.alicdn.com/kf/Hee2a7a6730c54787a8a6184a57d7ff44s.jpg)